
Урок 13.
Решение дифференциальных уравнений
Важное место в математических расчетах занимает решение дифференциальных уравнений. К нему, в частности, обычно относится анализ поведения различных систем во времени (анализ динамики), а также вычисление различных полей (тяготения, электрических зарядов и т. д.). Трудно переоценить роль дифференциальных уравнений в моделировании физических и технических объектов и систем, Maple 7 позволяет решать одиночные дифференциальные уравнения и системы дифференциальных уравнений как аналитически, так и в численном виде. Разработчиками системы объявлено о существенном расширении средств решения дифференциальных уравнений и о повышении их надежности в смысле нахождения решений для большинства классов дифференциальных уравнений. Поэтому данный урок целиком посвящен решению уравнений данного класса. Для решения системы простых дифференциальных уравнений (задача Коши) используется функция dsolve в разных формах записи:
dsolve(ODE)
dsolve(ODE, y(x), extra_args)
dsolve((ODE, ICs}, y(x), extra_args)
dsolve({sysODE, ICs}, {funcs}, extra_args)
Здесь ODE — одно обыкновенное дифференциальное уравнение или система из дифференциальных уравнений первого порядка с указанием начальных условий, у(х) — функция одной переменной, Ics — выражение, задающее начальные условия, {sysODE} —множество дифференциальных уравнений, {funcs} —множество неопределенных функций, extra_argument — опция, задающая тип решения. Параметр extra_argument задает класс решаемых уравнений. Отметим основные значения этого параметра:
Для решения задачи Коши в параметры dsolve надо включать начальные условия, а при решении краевых задач — краевые условия. Если Maple способна найти решение при числе начальных или краевых условий меньшего порядка системы, то в решении будут появляться неопределенные константы вида _С1, _С2 и т. д. Они же могут быть при аналитическом решении системы, когда начальные условия не заданы. Если решение найдено в неявном виде, то в нем появится параметр _Т.
По умолчанию функция dsolve автоматически выбирает наиболее подходящий метод решения дифференциальных уравнений. Однако в параметрах функции dsolve в квадратных скобках можно указать предпочтительный метод решения дифференциальных уравнений. Допустимы следующие методы:
| quadrature | linear | Bernoulli | separable |
|
inverse linear |
homogeneous |
Chini |
lin_sym |
| exact | Abel | pot_sym |
Информацию о каждом методе можно получить, используя команду Tdsolve, method и указав в ней конкретный метод. Например, команда Tdsolve,linear вызовет появление страницы справочной системы с подробным описанием линейного метода решения дифференциальных уравнений.
Производные при записи дифференциальных уравнений могут задаваться функцией diff или оператором D. Выражение sysODE должно иметь структуру множества и содержать помимо самой системы уравнений их начальные условия.
Начнем рассмотрение практических примеров с решения одиночных обыкновенных дифференциальных уравнений (ОДУ) первого порядка:
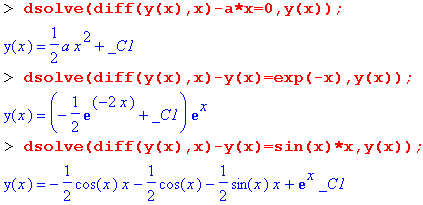
Следующие примеры иллюстрируют возможность решения одного и того же дифференциального уравнения ode_L разными методами:

Объем данной книги не позволяет остановиться на всех тонкостях аналитического решения дифференциальных уравнений. Множество примеров такого решения дано в справочной базе данных Maple,. 7- К ней нужно обратиться в случае, если решение того или иного дифференциального уравнения выходит за рамки учебного курса.
Решение дифференциальных уравнений второго порядка
Здесь видно, что для задания производной используется ранее рассмотренная функция diff. С помощью символа $ можно задать производную более высокого порядка. Ниже представлено решение двух дифференциальных уравнений второго порядка:
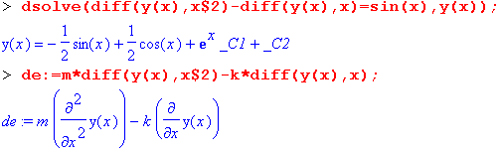

Обратите внимание на решение второго из этих уравнений. Здесь использован прием визуализации исходного дифференциального уравнения, и оно задается значением переменной de. Кроме того, и это особенно важно, решение осуществляется при заданных начальных условиях. Именно поэтому в решении отсутствуют произвольные постоянные вида _СN.
Решение систем дифференциальных уравнений
На рис. 13.1 представлено решение системы из двух дифференциальных уравнений различными методами — в явном виде, в виде разложения в ряд и с использованием преобразования Лапласа. Здесь следует отметить, что решение в виде ряда является приближенным. Поэтому полученные в данном случае аналитические выражения отличаются от явного решения и решения с применением преобразования Лапласа.

Рис. 13.1. Решение системы из двух дифференциальных уравнений различными методами
Следует отметить, что, несмотря на обширные возможности Maple 7 в области аналитического решения дифференциальных уравнений, оно возможно далеко не всегда. Поэтому, если не удается получить такое решение, полезно попытаться найти решение в численном виде.
Численное решение дифференциальных уравнений
Большинство нелинейных дифференциальных уравнений не имеет аналитического решения. Кроме того, часто аналитическое решение и не нужно, но требуется получить ответ в виде графических зависимостей.
В таких случаях для решения дифференциальных уравнений в численном виде используется функция dsolve с параметром numeric или type=numeric. При этом решение возвращается в виде специальной процедуры, по умолчанию реализующей широко известный метод решения дифференциальных уравнений Рунге—Кутта—Фелберга порядков 4 и 5 (в зависимости от условий адаптации решения к скорости его изменения). Эта процедура называется rkf45 и символически выводится (без тела) при попытке решения заданной системы дифференциальных уравнений. Последнее достаточно наглядно иллюстрирует рис. 13.2.
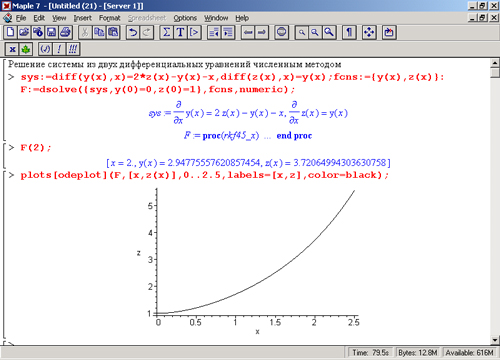
Рис. 13.2. Решение системы дифференциальных уравнений численным методом rkf45 с выводом графика решения
Указанная процедура возвращает особый тип данных, позволяющих найти решение в любой точке или построить график решения (или решений). Для графического отображения Maple 7 предлагает ряд возможностей, и одна из них представлена на рис. 13.2 — см. последнюю строку ввода. При этом используется функция plot[odeplot] из пакета odeplot, предназначенного для визуализации решений дифференциальных уравнений.
В список параметров функции dsolve можно явным образом включить указание на метод решения, например опция mathod=dverk78 задает решение непрерывным методом Рунге—Кутта порядка 7 или 8. Вообще говоря, численное решение дифференциальных уравнений можно производить одним из следующих методов:
Обилие используемых методов расширяет возможности решения дифференциальных уравнений в численном виде. Большинство пользователей Maple 7 вполне устроит автоматический выбор метода решения по умолчанию. Однако в сложных случаях возможна прямая установка одного из указанных выше методов. С деталями реализации методов можно ознакомиться по справочной системе.
С помощью параметра ' abserr' =аеrr можно задать величину абсолютной погрешности решения, а с помощью 'minerr'=mine — минимальную величину погрешности. В большинстве случаев эти величины, заданные по умолчанию, оказываются приемлемыми для расчетов.
Maple 7 реализует адаптируемые к ходу решения методы, при которых шаг решения h автоматически меняется, подстраиваясь под условия решения. Так, если прогнозируемая погрешность решения становится больше заданной, шаг решения автоматически уменьшается. Более того, система Maple способна автоматически выбирать наиболее подходящий для решаемой задачи метод решения.
Еще один пример решения системы дифференциальных уравнений представлен на рис. 13.3. Здесь на одном графике представлены зависимости у(х) и z(х), представляющие полное решение заданной системы. При этом процедура имеет особый вид listprocedure и для преобразования списка выходных данных в векторы решения Y и Z используется функция subs.
Для решения достаточно сложных задач полезны специальная структура DESol для решения дифференциальных уравнений и инструментальный пакет DEtools, содержащий самые изысканные средства для графической визуализации результатов решения дифференциальных уравнений. Эти средства мы более подробно рассмотрим в дальнейшем.
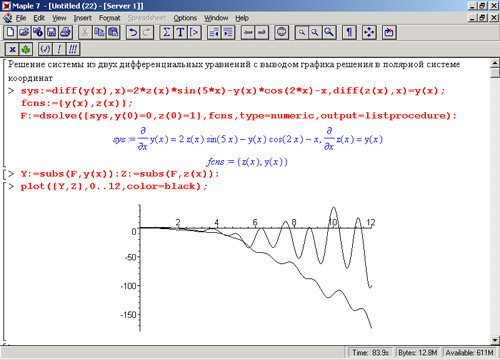
Рис. 13.3. Решение системы дифференциальных уравнений численным методом с выводом всех графиков искомых зависимостей
ВНИМАНИЕ
При решении некоторых задач физики и радиоэлектроники выбираемый поумолчанию шаг изменения аргументах или t - Л может привести к неустойчивости решения. Неустойчивости можно избежать рядом способов. Можно, например, нормировать уравнения, избегая необходимости использования малого шага. А можно задать заведомо малый шаг. Например, при method=classical для этого служит параметр stepsize-h. Примеры такого подхода будут даны в уроке 17 (см. Решение физических задач и моделирование цепи на туннельном диоде).
Дифференциальные уравнения с кусочными функциями
Функции кусочного типа широко используются при математическом моделировании различных физических объектов и систем. В основе такого моделирования обычно лежит решение дифференциальных уравнений, описывающих поведение объектов и систем. Покажем возможность применения кусочных функций для решения дифференциальных уравнений.
Ниже представлено задание дифференциального уравнения первого порядка, содержащего кусочную функцию:
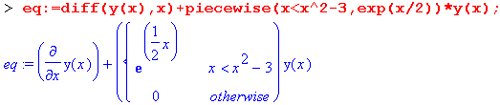
Используя функцию dsolve, выполним решение этого дифференциального уравнения:
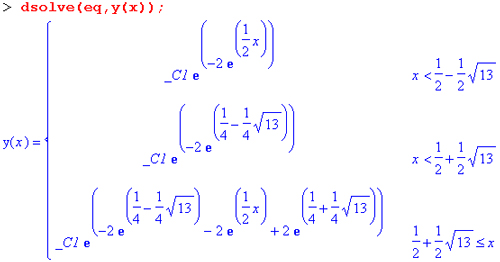
Нетрудно заметить, что результат получен также в форме кусочной функции, полностью определяющей решение на трех интервалах изменениях. Приведем пример решения дифференциального уравнения второго порядка с кусочной функцией:
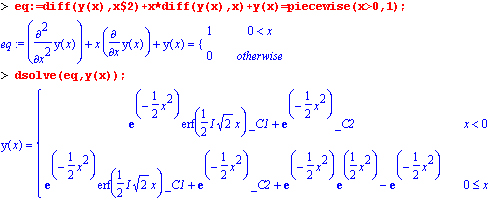
В конце этого раздела приведем пример решения нелинейного дифференциального уравнения Риккати с кусочной функцией:
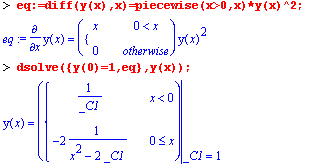
В ряде случаев желательна проверка решения дифференциальных уравнений. Ниже показано, как она делается для последнего уравнения:
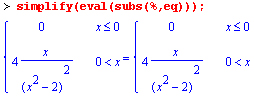
ПРИМЕЧАНИЕ
Как видно из приведенных достаточно простых и наглядных примеров, результаты решения дифференциальных уравнений с кусочными функциями могут быть довольно громоздкими. Это, однако, не мешает эффективному применению функций данного класса.
Структура неявного представления дифференциальных уравнений — DESol
В ряде случаев иметь явное представление дифференциальных уравнений нецелесообразно. Для неявного их представления в Maple 7 введена специальная структура:
DESol(expr.vars)
где exprs — выражение для исходной системы дифференциальных уравнений, vars — заданный в виде опции список переменных (или одна переменная). Структура DESol образует некоторый объект, дающий представление о дифференциальных уравнениях, чем-то напоминающее RootOf. С этим объектом можно обращаться, как с функцией, то есть его можно интегрировать, дифференцировать, получать разложение в ряд и вычислять численными методами. На рис. 13.4 показаны примеры применения структуры DESol. Обратите внимание на последний пример — в нем структура- DESol использована для получения решения дифференциального уравнения в виде степенного ряда.
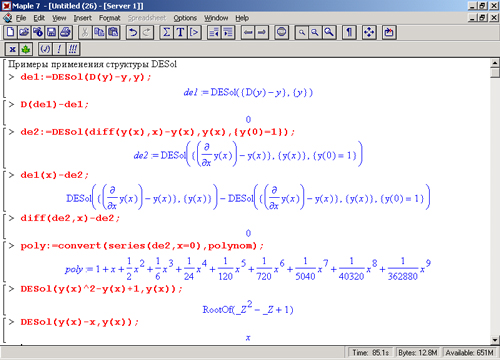
Рис. 13.4. Примеры применения структуры DESol
Инструментальный пакет решения дифференциальных уравнений DEtools
Решение дифференциальных уравнений самых различных типов — одно из достоинств системы Maple 7. Пакет DEtools предоставляет ряд полезных функций для решения дифференциальных уравнений и систем с такими уравнениями:
> with(DEtools);
Warning, the name adjoint has been redefined
[DEnormal, DEplot, DEplot3d, DEplot_pofygon, DFactor, DFactorLCLM, DFactorsols, Dchangevar, GCRD, LCLM, PDEchangecoords, RiemannPsols, Xchange, Xcommutator, Xgauge, abelsoL, adjoint, autonomous, bernoullisol, buildsol, buildsym, canoni, caseplqt, casesplit, checkrank, chinisol, clairautsol, constcoeffsols, convertAlg, convertsys, dalembertsol, dcoeffs, de2diffop, dfieldplot, diffop2de, dsubs, eigenring, endomorphism_charpoly, equinv, etajc, eulersols, exactsol, expsols, exterior'_power,firint,firtest, formal_sol, gen_exp, generate_ic, genhomosol, gensys, hamilton_eqs, indicialeq, infgen, initialdata, integrate_sols, intfactor, Invariants, kovacicsols, leftdivision, liesol, line_int, linearsol, matrixDE, matrix_riccati, moserjreduce, muchange, mult, mutest, newtonjpolygon, normalG2, odeadvisor, odepde, parametricsol, phaseportrait, poincare, polysols, ratsols, redode, reduceOrder, reduce_order, regular_parts, regularsp, remove_RootOf, riccati_system, riccatisol, rifsimp, rightdivision, rtaylor, separablesol, solvejgroup, super_reduce, symgen, symmetric_po\ver, symmetric^product, symtest, transinv, translate, untranslate, varparam, zoom]
Этот пакет дает самые изысканные средства для аналитического и численного решения дифференциальных уравнений и систем с ними. По сравнению с версией Maple V R5 число функций данного пакета в Maple 7 возросло в несколько раз. Многие графические функции пакета DEtools были уже описаны. Ниже приводятся полные наименования тех функций, которые есть в реализациях R5, 6 и 7 системы Maple:
Применение этих функций гарантирует совместимость документов реализаций Maple R5, 6 и 7.
Основные функции пакета DEtools
Ввиду обилия функций пакета DEtools дать их полное описание в данной книге не представляется возможным. Поэтому выборочно рассмотрим наиболее важные функции этого пакета. Функция:
autonomous(des.vars,ivar)
тестирует дифференциальное уравнение (или систему) des. Ее параметрами помимо des являются независимая переменная ivar и зависимая переменная dvar. Следующие примеры поясняют применение этой функции:
> automou(sin(z(t)-z(t)^2)*(D@@4)(z)(t)-cos(z(t))-5,z.t);
true
> DE:=diff(x(s),s)-x(s)*cos(arctan(x(s)))=arctan(s):
> autonomous(DE.{x},s);
false
Функция Dchangevar используется для обеспечения замен (подстановок) в дифференциальных уравнениях:
Dchangevar(trans,deqns, c_tvar, rMvar)
Dchangevar(tranl, tran2, .... tranN, deqns, c_ivar, n_ivar)
В первом случае trans — список или множество уравнений, которые подставляются в дифференциальное уравнение, список или множество дифференциальных уравнений deqns. При этом c_ivar — имя текущей переменной, n_ivar — имя новой переменной (его задавать необязательно). Во второй форме для подстановки используются уравнения tranl, tran2, .... Ниже представлены примеры применения функции Dchangevar:

Следует отметить, что подстановки являются мощным средством решения дифференциальных уравнений. Нередки случаи, когда дифференциальное уравнение не решается без их применения. Дополнительные примеры использования подстановок можно найти в справочной базе данных системы Maple 7.
Функция нормализации ОДУ DEnormal синтаксически записывается в виде:
DEnormal(des,ivar,dvar)
где des — система дифференциальных уравнений, 1var — независимая переменная и dvar — зависимая переменная. Применение этой функции поясняют следующие примеры:
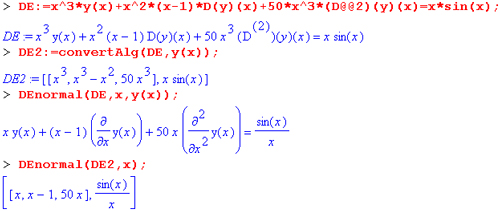
Функция convertAlg(des,dvar) возвращает список коэффициентов формы системы дифференциальных уравнений des с зависимыми переменными dvar. Это поясняют следующие примеры:
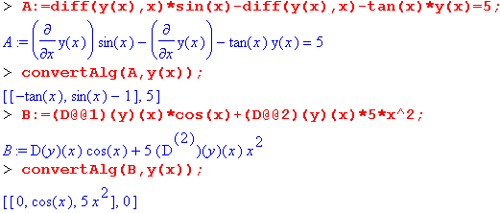
Для изменения переменных в системах дифференциальных уравнений используется функция convertsys:
convertsys(deqns, inits, vars, ivar, yvec, ypvec)
Здесь deqns — одно дифференциальное уравнение или список (множество), представляющие систему дифференциальных уравнений первого порядка, inits — множество или список начальных условий, vans — зависимые переменные, ivar — независимые переменные, yvec — вектор решений и ypvec — вектор производных. Функция:
indicialeq(des.ivar,alpha.dvar)
обеспечивает полиномиальное представление для линейного однородного дифференциального уравнения второго порядка des. Параметр alpha намечает точку сингулярности.
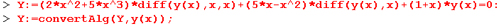

Функция:
reduceOrder(des.dvar,partsol, solutionForm)
обеспечивает понижение порядка дифференциального уравнения des (или системы уравнений, представленных списком или множеством) при зависимых переменных dvar, частном решении partsol (или списке частных решений) и флаге solutionForm, показывающем, что решение происходит явным методом (explicitly). Для демонстрации действия этой функции воспользуемся примером из ее справочной страницы:

Функция:
regularsp(des,ivar,dvar)
вычисляет регулярные особые (сингулярные) точки для дифференциального уравнения второго порядка или системы дифференциальных уравнений des. Следующий пример поясняет применение данной функции:
> coefs := [21*(х^2 - х + 1),0,100*х^2*(х-1)^2]:
> regularsp(coefs. х);
[0,1]
Еще две функции пакета DEtools:
translate(des,ivar.pt,dvar)
untranslate(des,ivar,pt,dvar)
выполняют особую операцию трансляции дифференциального уравнения (или списка дифференциальных уравнений) из центрированного относительно 0 в центрированное относительно 1 и наоборот. С деталями этого специфического процесса заинтересованный читатель может познакомиться в справочной базе данных. И еще одна полезная функция пакета:
varparam(sols.v.ivar)
находит общее решение дифференциального уравнения (или системы уравнений) sols методом вариации параметров. Параметр v задает правую часть уравнения; если он равен 0, ищется только частичное решение:

Более подробную информацию об этих функциях читатель найдет в их справочных страницах, а также в информационном документе detdols.mws содержащем систематизированное описание пакета DEtools с многочисленными примерами его применения.
Графическое представление решений дифференциальных уравнений
Применение функции odeplot пакета plots
Для обычного графического представления результатов решения дифференциальных уравнений может использоваться функция odeplot из описанного выше пакета plots. Эта функция используется в следующем виде:
odep1ot(s,vars.r,o)
где s — запись (в выходной фирме) дифференциального уравнения или системы дифференциальных уравнений, решаемых численно функцией dsolve, vars — переменные, г — параметр, задающий пределы решения (например, а. .Ь), и о — необязательные дополнительные опции.
На рис. 13.5 представлен пример решения одиночного дифференциального уравнения с выводом решения у(х) с помощью функции odeplot.
В этом примере решается дифференциальное уравнение:
y'(x)=cos(x2y(x))
при у(0) = 2 и x, меняющемся от-5 до 5. Левая часть уравнения записана с помощью функции вычисления производной diff. Результатом построения является график решения у(х).
В другом примере (рис. 13.6) представлено решение системы из двух нелинейных дифференциальных уравнений. Здесь с помощью функции odeplot строятся графики двух функций. —у(х) и z(x).
В этом примере решается система:
у'(х)=z(х),
z'(x) = 3 sin(y(x))
при начальных условиях y(0)=0, z(0) = 1 их, меняющемся от -4 до 4 при числе точек решения, равном 25.
Иногда решение системы из двух дифференциальных уравнений (или одного дифференциального уравнения второго порядка) представляется в виде фазового портрета — при этом по осям графика откладываются значения у(х) и z(х) при изменении х в определенных пределах. Рисунок 13.7 демонстрирует построение фазового портрета для системы, представленной выше.
Обычное решение, как правило, более наглядно, чем фазовый портрет решения. Однако для специалистов (например, в теории колебаний) фазовый портрет порою дает больше информации, чем обычное решение. Он более трудоемок; для построения, поэтому возможность Марle 7 быстро строить фазовые портреты трудно переоценить.
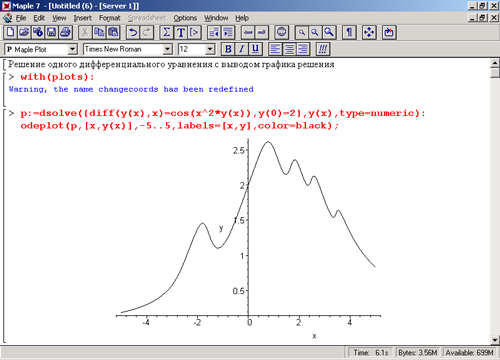
Рис. 13.5. Пример решения одиночного дифференциального уравнения
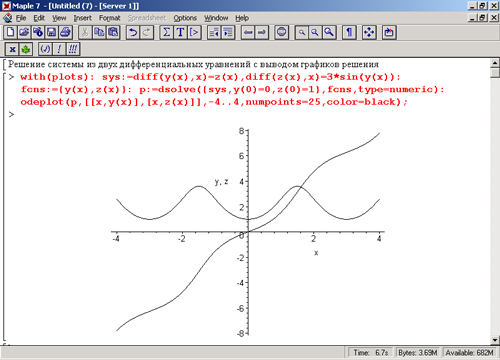
Рис. 13.6. Пример решения системы из двух дифференциальных уравнений
Рис. 13.7. Представление решения системы дифференциальных уравнений в виде фазового портрета
Функция DEplot из пакета DEtools
Специально для решения и визуализации решений дифференциальных уравнений и систем с дифференциальными уравнениями служит инструментальный пакет DEtools. В него входит ряд функций для построения наиболее сложных и изысканных графиков решения дифференциальных уравнений. Основной из этих функций является функция DEplot. Функция DEplot может записываться в нескольких формах:
DEplot(deqns, vars. trange. eqns)
DEplot(deqns, vans, trange. inits. eqns)
DEplot(deqns. vars. trange, уrange, xrgnge, eqns) .
DEplot(deqns. vars, trange. Inits, xrange. yrange, eqns)
Здесь deqns — список или множество, содержащее систему дифференциальных уравнений первого порядка или одиночное уравнение любого порядка; vars — зависимая переменная или список либо множество зависимых переменных; trange — область изменения независимой переменной t; Inits — начальные условия для решения; yrange — область изменения для первой зависимой переменной, xrange — область изменения для второй зависимой переменной; eqns — опция, записываемая в виде keyword-value. Замена имен переменных другими в данном случае недопустима.
Эта функция обеспечивает численное решение дифференциальных уравнений или их систем при одной независимой переменной t и строит графики решения. Для автономных систем эти графики строятся в виде векторного поля направлений, а для неавтономных систем — только в виде кривых решения. По умолчанию реализуется метод Рунге—Кутта 4-го порядка, что соответствует опции methodiclassical[rk4]. С функцией DEplot могут использоваться следующие параметры:
На рис. 13.8 показано решение системы диффкренциальных уравнений
x'(t)=x(t)(1-y(t)
y'(t)= 0,3y(t)(x(t)-1),
описывающих модель Лотки—Вольтерра при заданных в документе изменениях t, x(t) и y(t). Решение представлено в виде векторного поля стрелки которого являются касательными к кривым решения (сами эти кривые не строятся). Обратите внимание на функциональную закраску стрелок векторного поля, делающую решение особенно наглядным (правда, лишь на экране цветного дисплея, а не на страницах книги).
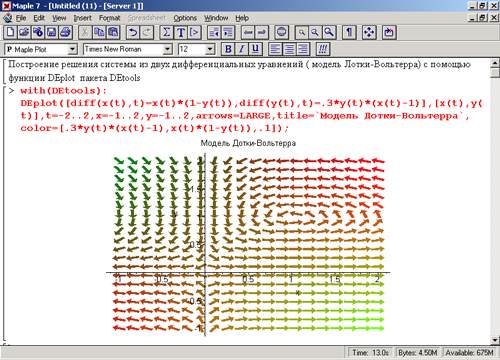
Рис. 13.8. Решение системы дифференциальных уравнений Лотки—Вольтерра , с выводом в виде графика векторного поля
Еще интересней вариант графиков, представленный на рис. 13.9. Здесь помимо векторного поля несколько иного стиля построены фазовые портреты решения с использованием функциональной закраски их линий. Фазовые портреты построены для двух наборов начальных условий:
x(0) = y(0) = 1,2 и x(0) = 1 и у(0)=0,7.
Следует отметить, что функция DEplot может обращаться к другим функциям пакета DEtools для обеспечения специальных графических возможностей, таких как построение векторного поля или фазового портрета решения.
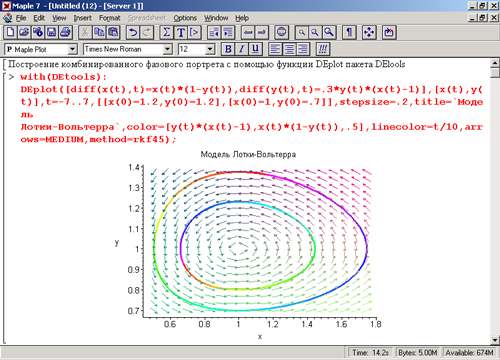
Рис. 13.9. Пример построения двух фазовых портретов на фоне векторного поля
Функция DEplotSd из пакета DEtools
В ряде случаев решение систем дифференциальных уравнений удобно представлять в виде пространственных кривых — например, линий равного уровня или просто в виде кривых в пространстве. Для этого служит функция DEplot3d:
DEplot3d(deqns, vars, trarige, initset, о)
DEplot3d(deqns, vars, trang, yrange, xrange, initset, o)
Назначение параметров этой функции аналогично указанному для функции DEplot.
Рисунок 13.10 поясняет применение функции DEPlqt3d для решения системы из двух дифференциальных уравнений с выводом фазового портрета колебаний в виде параметрически заданной зависимости x(t), y(t). В данном случае фазовый портрет строится на плоскости по типу построения графиков/линий равной высоты.
Другой пример (рис. 13.11) показывает решение системы из двух дифференциальных уравнений с построением объемного фазового портрета. В этом случае используется трехмерная координатная система и графические построения соответствуют параметрическим зависимостям x(t), y(t) и z(t). Вид фазового портрета напоминает разворачивающуюся в пространстве объемную, спираль.
Функциональная окраска делает график пикантным.
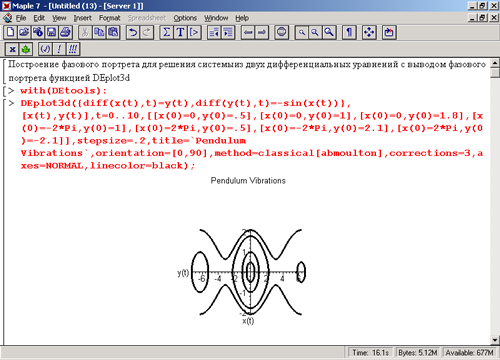
Рис. 13.10. Пример решения системы из двух дифференциальных уравнений с помощью функции DEptot3d
Возможности функции DEplot3d позволяют решать системы, состоящие более чем из двух дифференциальных уравнений. Однако в этом случае число решений, представляемых графически, выходит за пределы возможного для трехмерной графики. При этом от пользователя зависит, какие из зависимостей опускаются при построении, а какие строятся.
Функция PDEplot пакета DEtools
Еще одна функция пакета DEtools — DEtools[PDEp1ot] — служит для построения графиков решения систем с квазилинейными дифференциальными уравнениями первого порядка в частных производных.
Эта функция используется в следующем виде:
PDEplotCpdiffeq, van, i_curve, srange, о)
PDEplot(pdiffeq, var, i_curve. srange, xrange, yrange, urange, o)
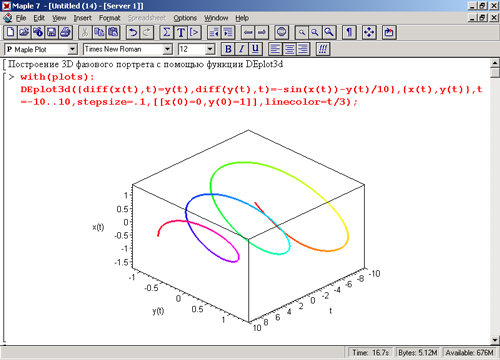
Рис. 13.11. Пример решения системы из двух дифференциальных уравнений с построением трехмерного фазового портрета
Здесь помимо упоминавшихся ранее параметров используются следующие: pdiffeq — квазилинейные дифференциальные уравнения первого порядка (PDE), vans — независимая переменная и i_curve — начальные условия для параметрических кривых трехмерной поверхности. Помимо опций, указанных для функции DEplot, здесь могут использоваться следующие опции:
Рисунок 13.12 демонстрирует применение функции PDEplot. Этот пример показывает, насколько необычным может быть решение даже простой системы дифференциальных уравнений в частных производных.
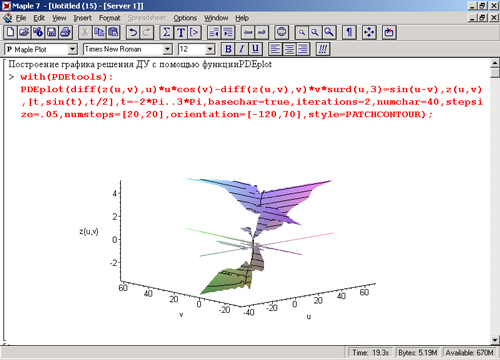
Рис. 13.12. Пример применения функции PDEplot
В данном случае решение представлено трехмерной фигурой весьма нерегулярного вида.
Другой пример использования функции PDEplot показан на рис. 13.13. Он иллюстрирует комбинированное построение графиков решения разного типа с применением функциональной закраски, реализуемой по заданной формуле с помощью опции initcolor.
Еще раз отметим, что, к сожалению, рисунки в данной книге не дают представления о цвете выводимого Maple графика. Поэтому наглядность решений, видимых на экране монитора, существенно выше.
Графическая функция dfieldplot
Графическая функция dfieldplot служит для построения поля направления с помощью векторов по результатам решения дифференциальных уравнений. Фактически эта функция как бы входит в функцию DEplot и при необходимости вызывается последней. Но она может использоваться и самостоятельно, что демонстрирует рис. 13.14, на котором показан пример решения следующей системы дифференциальных уравнений:
x'(t) =x(t)(1- y(t)),
y'(t) = 0,3y(t)(x(t) - 1).
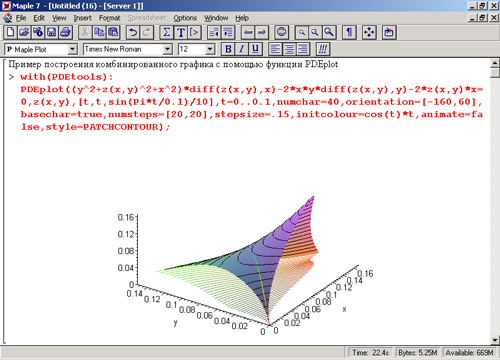
Рис. 13.13. Построение комбинированного графика с помощью функции PDEplot
Обратите внимание на использование опций в этом примере, в частности на вывод надписи на русском языке. В целом список параметров функции phaseportrait аналогичен таковому для функции DEplot (отсутствует лишь задание начальных условий).
Графическая функция phaseportrait
Графическая функция phaseportrait служит для построения фазовых портретов по результатам решения одного дифференциального уравнения или системы дифференциальных уравнений deqns. Она задается в следующем виде:
phaseportrait(deqns,vars,traf,1n1ts,o)
При задании уравнений достаточно указать их правые части. На рис. 13.15 представлен пример применения функции phaseportrait для решения системы из трех дифференциальных уравнений первого порядка.
В этом примере система дифференциальных уравнений задана с помощью оператора дифференцирования D. Функциональная окраска линии фазового портрета достигается использованием параметра linecolor, в правой части которого задана формула для цвета.
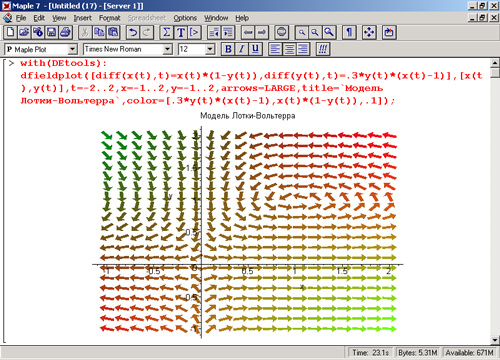
Рис. 13.14. Построение фазового портрета в виде графика векторного поля
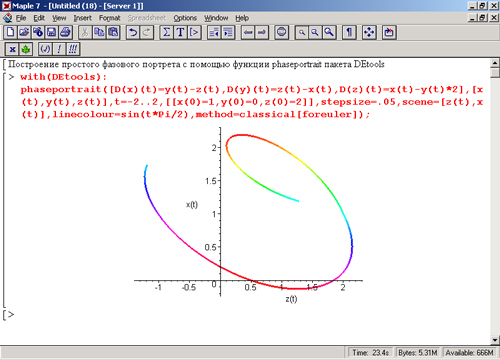
Рис. 13.15. Построение фазового портрета с помощью функции phaserportrait
Еще более интересный пример решения дифференциального уравнения представлен на рис. 13.16. Здесь построены фазовые портреты для асимптотических решений.
В целом надо отметить, что возможности визуализации решений дифференциальных уравнений с помощью системы Maple 7 весьма велики и приведенные выше примеры лишь частично иллюстрируют сказанное. В справочной системе можно найти ряд других весьма эффектных решений систем дифференциальных уравнений с визуализацией последних. ,
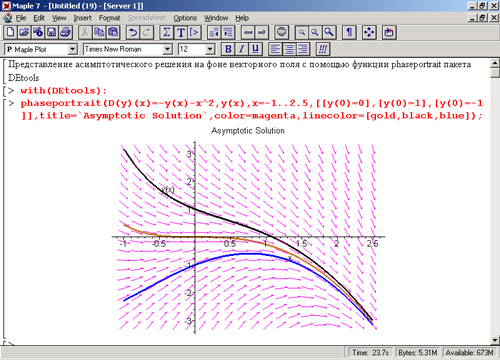
Рис. 13.16. Построение асимптотического решения на фоне графика векторного поля
Углубленный анализ дифференциальных уравнений
Задачи углубленного анализа ДУ
Maple 7 существенно доработана по части решения дифференциальных уравнений (ДУ) и систем с ДУ. Эта доработка прежде всего направлена на получение верных решений как можно большего числа ДУ разных классов и систем с ДУ.
В частности, расширен круг нелинейных дифференциальных уравнений, для которых Maple7способна дать аналитические решения.
Весь арсенал средств решения ДУ-и методика их применения вполне заслуживают отражения в отдельной большой книге. Мы ограничимся описанием только трех средств системы Maple 7 - проверки ДУ на автономность, углубленным анализом решения с помощью контроля уровня выхода и получением приближенного полиномиального аналитического решения. Более подробное знакомство с новыми возможностями решения дифференциальных уравнений можно получить из соответствующей статьи справки symbolics в разделе What is new.
Одиночное дифференциальное уравнение или система дифференциальных уравнений называются автономными, если их правая часть явно не зависит от независимой переменной. Для автономных дифференциальных уравнений или систем при построении графиков решений функцией DEplot не обязательно задавать начальные условия, но нужно указывать диапазон изменения искомых переменных.
Для проверки уравнений (или систем) на автономность используется функция:
autonomous(des,vars,ivar)
где des — заданное дифференциальное уравнение или (в виде списка) система дифференциальных уравнений, vars — зависимые переменные; ivar — независимая переменная. Если система автономна, то эта функция возвращает true, в противном случае false.
Примеры:
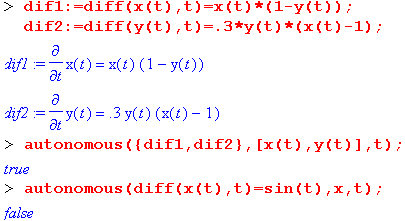
В первом случае система дифференциальных уравнений (модель. Лотки-Воль-терра) автономна, а во втором случае дифференциальное уравнение не автономно.
Контроль уровня вывода решения ДУ
Для углубленного анализа аналитического решения ДУ (или системы ДУ) можно использовать специальную возможность управления уровнем вывода решения с помощью системной переменной infilevel(dsolve)=level. Значение level =all дает обычный вывод решения без Комментариев, уровень 1 зарезервирован для информации, которую может сообщить пользователь, уровень 2 или 3 дает более детальный вывод (включая сообщения об использованном алгоритме и технике решения) и, наконец, уровни 4 и 5 дают наиболее детальную информацию (если тиковая есть в дополнение к той информации, которую дает уровень 2 или 3).
Приведем пример .аналитического решения ДУ третьего порядка с контролем уровня вывода решения:


В данном случае повышение уровня вывода до 4 или 5 бесполезно, поскольку вся информация о решении сообщается уже при уровне 2 (или 3).
Приближенное полиномиальное решение ДУ
Во многих случаях аналитические решения даже простых ДУ оказываются весьма сложными, например содержат специальные математические функции. При этом нередко полезна подмена такого решения другим, тоже аналитическим, но приближенным решением. Наиболее распространенным приближенным решением в этом случае может быть полиномиальное решение, то есть замена реального решения полиномом той или иной степени. При этом порядок полинома задается значением системной переменной Order, а для получения такого решения функция dsolve должна иметь параметр series.
На рис. 13.17 представлено решение ДУ третьего порядка различными методами: точное аналитическое и приближенное в виде полинома с максимальным заданным порядком 10 и 60. График дает сравнение этих решений для зависимости y(t).
Дадим небольшой комментарий. Нетрудно заметить, что точное аналитическое решение весьма сложно и содержит специальные функции Бесселя и гамма- функции. При порядке полинома 8 (он несколько меньше заданного максимального) решение практически совпадает с точным до значений t < 2, а при максимальном заданном порядке 60 область совпадения расширяется до значений t < 5,5. Затем приближенное решение резко отходит от точного.
Этот пример, с одной стороны, иллюстрирует хорошо известный факт — быстрое нарастание погрешности полиномиального приближения за пределами области хорошего совпадения решений. С другой стороны, он показывает, что степень полинома более 60 (и даже выше) вовсе не так уж бесполезна, как это утверждается во многих статьях и книгах по полиномиальному приближению. Точность полиномиальных вычислений Maple 7 достаточно высока, чтобы обеспечить получение приближенных полиномиальных выражений со степенью порядка десятков и иногда даже сотен. Другое дело, что столь «длинный» полином не всегда удобен для аналитических расчетов, даже несмотря на его структурную простоту.
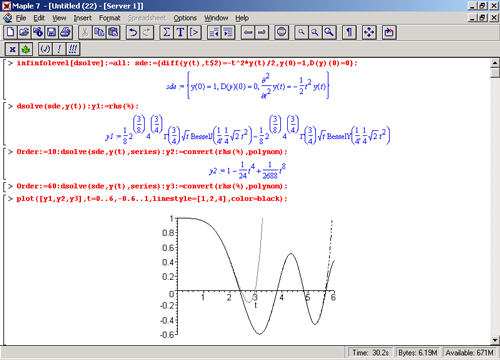
Рис. 13.17. Примеры решения ДУ третьего порядка
В этим уроке мы научились: